When we want to know whether cells in an excel spreadsheet are empty or not, we can use the excel ISBLANK function. This function returns TRUE if the cell is empty, and FALSE if not empty. This post provides a clear guide on how to use the Excel ISBLANK function.
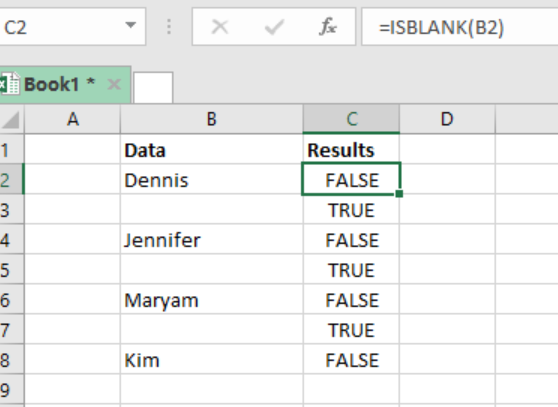Figure 1: Excel ISBLANK function
Syntax of the formula
=ISBLANK (value)
Where;
- Value- refers to the value we want to check. Can be a cell reference.
Explanation of the Excel ISBLANK function
The ISBLANK function is necessary when we want to easily know those cells that are blank and those that are not in excel. We get the following results from the function;
- The function will return TRUE if the cell is empty.
- FALSE if the cell is not empty.
We can look at the ISBLANK as meaning “is empty”, as it will return a TRUE if the cell is actually empty.
Note that anything that can be in a cell, whether an empty string or a formula, the ISBLANK function will return FALSE.
Example
Figure 2: Examining empty and non-empty cells using ISBLANK function
Step 1: Prepare the excel sheet you want to examine.
Step 2: In cell B2, specify the formula, i.e. =ISBLANK (A2). Note that A2 is a cell reference for our value.
Step 3: Press Enter to get the result.
Step 4: Copy down the formula to get result for the other cells.
Instant Connection to an Expert through our Excelchat Service
Most of the time, the problem you will need to solve will be more complex than a simple application of a formula or function. If you want to save hours of research and frustration, try our live Excelchat service! Our Excel Experts are available 24/7 to answer any Excel question you may have. We guarantee a connection within 30 seconds and a customized solution within 20 minutes.
Leave a Comment